开普勒第三定律

    定律表述

   开普勒第三定律也叫行星运动定律，其表述是：绕以太阳为焦点的椭圆轨道运行的所有行星

，其各自椭圆轨道半长轴的立方与周期的平方之比是一个常量。也就是：绕同一中心天体的所

有行星的轨道的半长轴的三次方（a³）跟它的公转周期的二次方（T²）的比值都相等，即

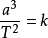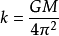， （其中M为中心天体质量，k为开普勒常数，这是一个只与被绕星体有关的常量，G为引力常量，其2006年国际推荐数值为G=6.67428×10⁻¹¹N·m²/kg²

德国天文学家约翰尼斯·开普勒根据丹麦天文学家第谷·布拉赫等人的观测资料和星表，通过开普勒本人的观测和分析后，于1609年在他出版的《新天文学》上发表了关于行星运动的前两条定律，又于1618年，在《宇宙谐和论》提出了第三条定律。

数学证明

我们用A，B分别为行星运动的近日点和远日点，以 和 分别表示行星在该点的速度，由于速度沿轨道切线方向，可见 和 的方向均与此椭圆的长轴垂直，则行星在此两点时对应的面积速度分别为

………………{1}

根据开普勒第二定律，应有

，因此得

…………………………………{2}

行星运动的总机械能E等于其动能与势能之和，则当他经过近日点和远日点时，其机械能应分别为

…………{3}

根据机械能守恒，应有 ，故得

……………{4}

由{2}{4}两式可解得

………………………………{5}

由{5}式和{1}式得面积速度为

椭圆的面积为 ,则得此行星运动周期为

…………………………{6}

将{6}式两边平方，便得

注： 是半长轴， 是半短轴， 是半焦距 

适用范围

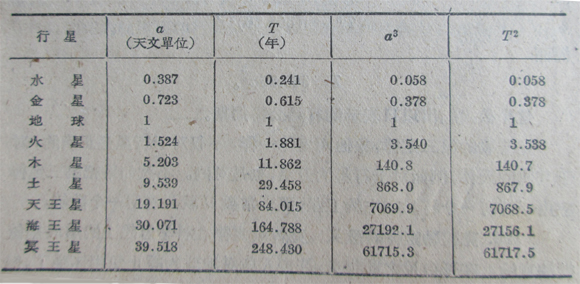
开普勒定律是一个普适定律，适用于一切二体问题。开普勒定律不仅适用于太阳系，他对具有中心天体的引力系统（如行星-卫星系统）和双星系统都成立。围绕同一个中心天体运动的几个天体，它们轨道半径三次方与周期的平方的比值（R³/T²）都相等，为（GM/4π²），为中心天体质量。这个比值是一个与行星无关的常量，只与中心体质量有关，那么M相同是这个比值相同